The Bullvine is often asked, “How can using genomic sires be better, if the genomic sire’s reliabilities are not as high as those for proven sires?” So in typical Bullvine style we set out to answer that question. The following is our answer…
Single Trait – Fat
Bullvine wanted to keep this comparison as simple as possible. To do this we used one trait, in this case fat yield, knowing that breeders do not select for one trait only. The results apply to all traits.
Females in Your Barn
You have a virgin heifer and a seven year old cow that are both indexed at 100 kgs for fat yield. Both have been genomically tested and the cow is milking in her fourth lactation. The heifer’s index is 67% Rel. and the cow is 82% Rel.
TABLE 1: Females
| Born | Fat Index | % Rel | Regressed Fat Index | |
| Heifer | 2012 Jan 10 | 100 | 67 | 67 |
| Cow | 2005 Jan 16 | 100 | 82 | 82 |
Sires
Three sires you might consider using for breeding these females could be:
TABLE 2: Sires
| Born | Fat Index (kgs) | % Rel | Regressed Fat Index | |
| Oman | March 08, 1998 | 82 | 99 | 81 |
| Supersire | Dec 28, 2010 | 116 | 67 | 78 |
| Pride | January 27, 2012 | 135 | 69 | 93 |
Index of Calves
What will be the fat indexes for the resulting calves? (Add parents together and divide by two)
TABLE 3: Regressed Fat Indexes for Calves (kgs)
| DAMS | SIRES | ||
| OMAN | SUPERSIRE | PRIDE | |
| Heifer | 74 | 72.5 | 80 |
| Cow | 81.5 | 80 | 87.5 |
These values are the expected average fat indexes. And, yes, there will be less variation amongst the progeny for Oman and the cow. The most variability amongst the progeny can be expected for the heifer when mated to Supersire or Pride.
Therefore, the short answer for which bull to use, is Pride. Pride will maximize the calf’s fat yield index.
Rate of Genetic Gain
Determining genetic gain is a principle taught to all college genetic students. The formula is:
Let’s simplify this:
Accuracy = Reliability
Selection Intensity = Determined by where the animal ranks in the population (all these animals are in the top 1% of the population so their selection intensity is identical)
Genetic Variation = Standard Deviation of fat yield indexes (common for all the animals in the example)
Generation Interval = The average time between the birth of the parents and the birth of the calf.
Generation Interval is the place where the numbers for the heifer and the sires, Supersire and Pride, are much smaller (in years) than those for the cow and Oman.
TABLE 4: Generation Interval (years)
| DAMS | SIRES | ||
| OMAN | SUPERSIRE | PRIDE | |
| Heifer | 8.5 | 2.5 | 2.0 |
| Cow | 11.5 | 5.5 | 5.0 |
Since the numbers for fat index in TABLE 3 are all similar, dividing them by a larger vs. a smaller generation interval greatly affects the outcome for genetic gain.
For the cow and Oman dividing 81.5 (Fat Index) by 11.5 (Generation Interval) gives a much smaller gain than for the heifer and Pride (80 divided by 2.0). In fact it is much different 7.9 compared to 40.
That’s the reason turning generations more quickly, using genomics, gives the faster rates of annual genetic gain. (Read more: The Genomic Advancement Race – The Battle for Genetic Supremacy)
The Bullvine Bottomline
Genomics gives you more speed. No question. If you’re worried about speed being dangerous, spread the risk by using multiple (not one) high indexing genomic sires where you might have only used one or two proven sires in the past.
Get original “Bullvine” content sent straight to your email inbox for free.








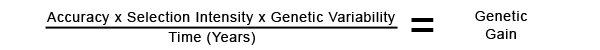










I don’t think that the variation in the progeny of one genomic sire is necessarily more than that of one proven sire. However, the average compared to the expected outcome (genomic proof) will have more variation for a genomic sire than a proven sire. This means there will be more variation in progeny from a group of genomic sires than a group of proven sires.
A proof doesn’t indicate the range possible for progeny but only the average, so a proven sire may have a high average but also wide variation meaning there will be some outstanding progeny but also some poor progeny.